Programação dinâmica: exemplos, problemas comuns e soluções
Não há dúvida de que os problemas de programação dinâmica podem ser muito intimidantes em uma entrevista de codificação. Mesmo quando você sabe que um problema precisa ser resolvido usando um método de programação dinâmico, é um desafio ser capaz de chegar a uma solução funcional em um período de tempo limitado.
A melhor maneira de ser bom em problemas de programação dinâmica é passar por tantos deles quanto possível. Embora você não precise necessariamente memorizar a solução para cada problema, é bom ter uma ideia de como implementar uma.
O que é programação dinâmica?
Simplificando, a programação dinâmica é um método de otimização para algoritmos recursivos, muitos dos quais são usados para resolver problemas de computação ou matemáticos.
Você também pode chamá-la de técnica algorítmica para resolver um problema de otimização dividindo-a em subproblemas mais simples. Um princípio fundamental no qual a programação dinâmica se baseia é que a solução ótima para um problema depende das soluções para seus subproblemas.
Sempre que vemos uma solução recursiva que tem chamadas repetidas para as mesmas entradas, podemos otimizá-la usando a programação dinâmica. A ideia é simplesmente armazenar os resultados dos subproblemas para que não tenhamos que recalculá-los quando necessário posteriormente.
Soluções programadas dinamicamente têm uma complexidade polinomial que garante um tempo de execução muito mais rápido do que outras técnicas como recursão ou retrocesso. Na maioria dos casos, a programação dinâmica reduz as complexidades do tempo, também conhecidas como big-O , de exponencial para polinomial.
Agora que você tem uma boa ideia do que é programação dinâmica, é hora de verificar alguns problemas comuns e suas soluções.
Problemas de programação dinâmica
1. Problema da mochila
Declaração do Problema
Dado um conjunto de itens, cada um com um peso e um valor, determine o número de cada item a ser incluído em uma coleção de modo que o peso total não exceda um determinado limite e o valor total seja o maior possível.
São fornecidos dois valores de matrizes inteiras [0..n-1] e pesos [0..n-1] que representam valores e pesos associados a n itens, respectivamente. Também é fornecido um inteiro W que representa a capacidade da mochila.
Aqui, estamos resolvendo o problema da mochila 0/1, o que significa que podemos escolher adicionar um item ou excluí-lo.
Algoritmo
- Crie uma matriz bidimensional com n + 1 linhas e w + 1 colunas. Um número de linha n denota o conjunto de itens de 1 a i , e um número de coluna w denota a capacidade máxima de carga da sacola.
- O valor numérico em [i] [j] denota o valor total de itens até i em uma sacola que pode carregar um peso máximo de j.
- Em cada coordenada [i] [j] na matriz, escolha o valor máximo que podemos obter sem o item i , ou o valor máximo que podemos obter com o item i — o que for maior.
- O valor máximo que pode ser obtido com a inclusão do item i é a soma do próprio item i e o valor máximo que pode ser obtido com a capacidade restante da mochila.
- Execute esta etapa até encontrar o valor máximo para a W ª linha.
Código
def FindMax(W, n, values, weights):
MaxVals = [[0 for x in range(W + 1)] for x in range(n + 1)]
for i in range(n + 1):
for w in range(W + 1):
if i == 0 or w == 0:
MaxVals[i][w] = 0
elif weights[i-1] <= w:
MaxVals[i][w] = max(values[i-1]
+ MaxVals[i-1][w-weights[i-1]],
MaxVals[i-1][w])
else:
MaxVals[i][w] = MaxVals[i-1][w]
return MaxVals[n][W]
2. Problema de troca de moeda
Declaração do Problema
Suponha que você tenha uma matriz de números que representa os valores de cada moeda. Dado um valor específico, encontre o número mínimo de moedas necessárias para fazer esse valor.

Algoritmo
- Inicialize uma matriz de tamanho n + 1 , onde n é a quantidade. Inicialize o valor de cada índice i na matriz para ser igual ao valor. Isso denota o número máximo de moedas (usando moedas de denominação 1) necessárias para perfazer esse montante.
- Visto que não há denominação para 0, inicialize o caso base onde array [0] = 0 .
- Para cada outro índice i , comparamos o valor nele (que é inicialmente definido como n + 1 ) com o array de valores [ik] +1 , onde k é menor que i . Isso essencialmente verifica todo o array até i-1 para encontrar o número mínimo possível de moedas que podemos usar.
- Se o valor em qualquer matriz [ik] + 1 for menor que o valor existente na matriz [i] , substitua o valor na matriz [i] por aquele na matriz [ik] +1 .
Código
def coin_change(d, amount, k):
numbers = [0]*(amount+1)
for j in range(1, amount+1):
minimum = amount
for i in range(1, k+1):
if(j >= d[i]):
minimum = min(minimum, 1 + numbers[jd[i]])
numbers[j] = minimum
return numbers[amount]
3. Fibonacci
Declaração do Problema
A Série de Fibonacci é uma sequência de inteiros onde o próximo inteiro na série é a soma dos dois anteriores.
É definido pela seguinte relação recursiva: F (0) = 0, F (n) = F (n-1) + F (n-2) , onde F (n) é o enésimo termo. Neste problema, temos que gerar todos os números em uma seqüência de Fibonacci até um determinado n- ésimo termo.
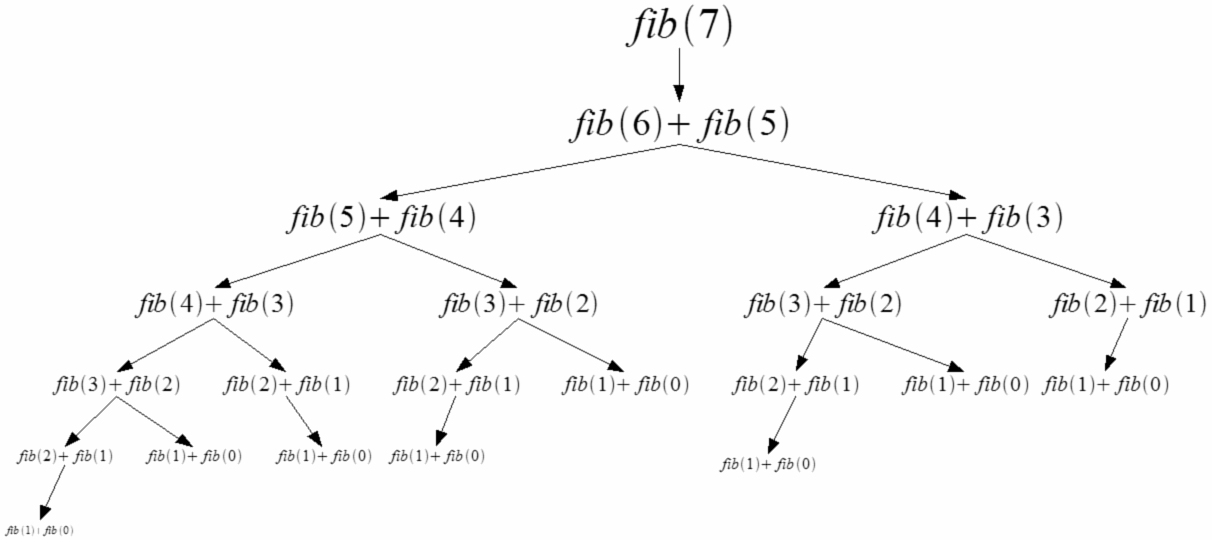
Algoritmo
- Primeiro, use uma abordagem recursiva para implementar a relação de recorrência fornecida.
- Resolver esse problema recursivamente envolve quebrar F (n) em F (n-1) + F (n-2) e, em seguida, chamar a função com F (n-1) e F (n + 2) como parâmetros. Fazemos isso até que os casos básicos em que n = 0 ou n = 1 sejam alcançados.
- Agora, usamos uma técnica chamada memoização. Armazene os resultados de todas as chamadas de função em uma matriz. Isso garantirá que para cada n, F (n) só precisa ser calculado uma vez.
- Para quaisquer cálculos subsequentes, seu valor pode simplesmente ser recuperado da matriz em tempo constante.
Código
def fibonacci(n):
fibNums = [0, 1]
for i in range(2, n+1):
fibNums.append(fibNums[i-1] + fibNums[i-2])
return fibNums[n]4. Subseqüência de aumento mais longa
Declaração do Problema
Encontre o comprimento da maior subsequência crescente dentro de um determinado array. A maior subsequência crescente é uma subsequência dentro de um array de números com uma ordem crescente. Os números dentro da subsequência têm que ser únicos e em ordem crescente.
Além disso, os itens da sequência não precisam ser consecutivos.
Algoritmo
- Comece com uma abordagem recursiva onde você calcula o valor da maior subsequência crescente de cada subarray possível do índice zero ao índice i, onde i é menor ou igual ao tamanho do array.
- Para transformar esse método em dinâmico, crie uma matriz para armazenar o valor de cada subsequência. Inicialize todos os valores desta matriz para 0.
- Cada índice i deste array corresponde ao comprimento da maior subsequência crescente para um subarray de tamanho i .
- Agora, para cada chamada recursiva de findLIS (arr, n), verifique o th n índice do array. Se este valor for 0, então calcular o valor com o método referido no primeiro passo e armazená-lo no th n índice.
- Finalmente, retorne o valor máximo da matriz. Este é o comprimento da maior subsequência crescente de um determinado tamanho n .
Código
def findLIS(myArray):
n = len(myArray)
lis = [0]*n
for i in range (1 , n):
for j in range(0 , i):
if myArray[i] > myArray[j] and lis[i]< lis[j] + 1 :
lis[i] = lis[j]+1
maxVal= 0
for i in range(n):
maxVal = max(maxVal , lis[i])
return maxValSoluções para problemas de programação dinâmica
Agora que você já passou por alguns dos problemas de programação dinâmica mais populares, é hora de tentar implementar as soluções sozinho. Se você estiver travado, pode sempre voltar e consultar a seção de algoritmo para cada problema acima.
Considerando o quão populares são as técnicas, como recursão e programação dinâmica, hoje, não custa nada verificar algumas plataformas populares onde você pode aprender esses conceitos e aprimorar suas habilidades de codificação . Embora você não tenha esses problemas diariamente, certamente os encontrará em uma entrevista técnica.
Naturalmente, ter o know-how de problemas comuns certamente renderá dividendos na sua próxima entrevista. Portanto, abra seu IDE favorito e comece!

