Teorema de Turing: é por isso que nenhum algoritmo pode nos dizer se uma IA agirá contra a humanidade

dezembro 8, 2023 gurinho

Estamos em meados de janeiro de 2021 quando um relatório do Instituto Max Planck aparece no Journal of Artificial Intelligence Research que destaca como uma Super IA equipada com capacidades de autoaprendizagem (super algoritmo) poderia escapar do controle de seus programadores e, virtualmente/ hipoteticamente, levaria o gênero Homo Sapiens à extinção. Neste artigo pretendemos destacar a inexistência teórica (Teorema da Incompletude de Alan Turing ) de um algoritmo que possa decidir se uma IA pode agir contra a Humanidade.

Teorema de Turing: premissa

Esta localização é presumivelmente inadequada até mesmo para uma ilustração elementar dos Teoremas de Gödel e Turing devido à sua complexidade lógica intrínseca; o que, por outro lado, é interessante é como ambos os teoremas fazem uso da autorreferencialidade.

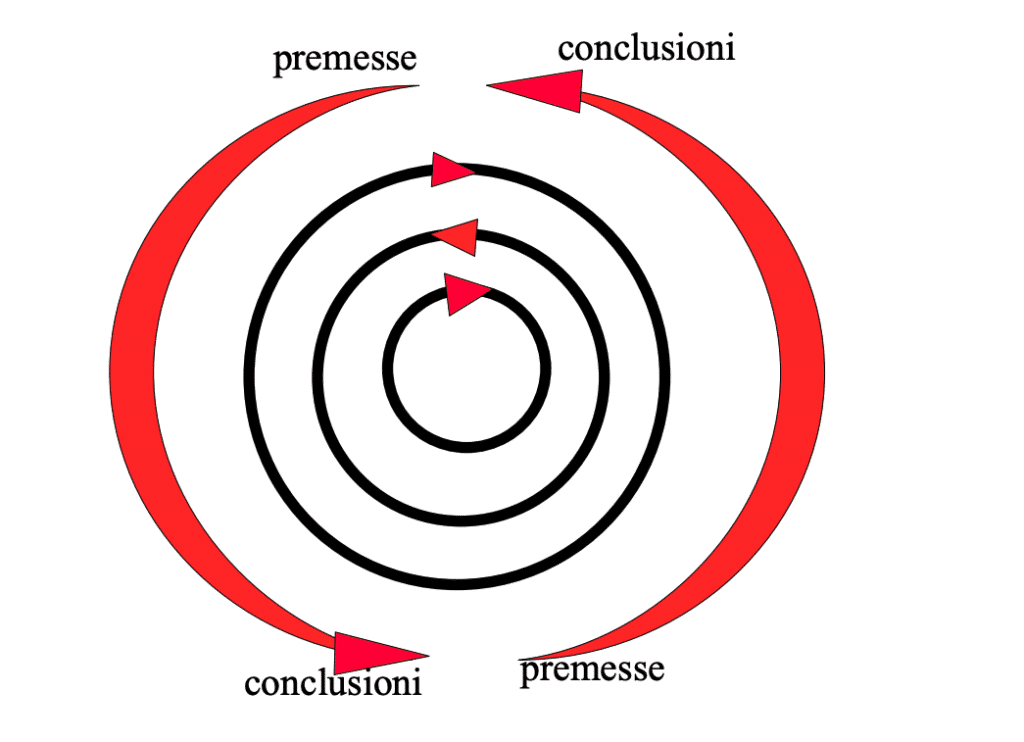
Nota : Auto-referencialidade = Dialelo (diallelos do grego = raciocínio circular) indica uma pseudo-prova lógica onde as conclusões derivam das hipóteses iniciais que, por sua vez, são obtidas diretamente das conclusões. No léxico comum: “cobra que come o próprio rabo”

Paradoxo do mentiroso

As informações relatadas neste site são sempre falsas.

É sabido, desde a sua enunciação (Eubulides de Mileto século IV a.C.), como esta afirmação conduz inevitavelmente ao Paradoxo do Mentiroso. Aqui é interessante destacar seu conteúdo auto-referencial-circular (potencialmente recursivo) que conduz às etapas subsequentes do tipo:

if (a informação é sempre falsa = A) então (a informação de que a informação é sempre falsa = B também é falsa)
se (a informação de que a informação é sempre falsa também é falsa = B) então (é verdade que a informação é sempre falsa = A)

0 = falso 1 = verdadeiro

se A = 0 então B = 0

se B = 0 então A = 0

Simbolicamente, A leva a B e B, por sua vez, leva a A.

O Paradoxo do Mentiroso foi proposto, ao longo do tempo, em várias formas logicamente idênticas, embora formalmente diferentes, por uma grande variedade de autores: Aristóteles, Diógenes, Buridan, Cervantes, etc. A solução para o paradoxo proposta por Aristóteles levanta a hipótese de que ele é gerado pela confusão entre um termo (falsificar) e sua citação (falso) (que não acrescenta nenhuma contribuição lógica) ao primeiro termo.

William de Ockham argumenta que o paradoxo é gerado pela fusão entre linguagem e metalinguagem onde a frase “a informação é sempre falsa” é escrita em metalinguagem. Da mesma forma para Alfred Tarski (1944) que o Paradoxo é gerado pela autonímia (uma metalinguagem que ainda indica a si mesmo).

O paradoxo de Richard

O Paradoxo de Richard (Jules Antoine Richard – 1905) é de muito maior importância. Considere definir rigorosa e completamente todas as propriedades dos números inteiros racionais. Por exemplo:

número primo = divisível apenas por ele mesmo e pela unidade
quadrado perfeito = produto de um número por ele mesmo
número par = divisível por dois
número irracional = não pode ser representado como uma fração de inteiros racionais
etc.

Para qualquer axiomatização da Aritmética o número de propriedades dos Inteiros Racionais é em quantidade finita de modo que a sua ordenação segundo um critério arbitrário e a consequente numeração progressiva conduzirão a uma sequência numerada finita. Por exemplo:

1-inteiro = união entre naturais positivos e negativos
2 quadrados perfeitos = produto de um número por ele mesmo
3 números ímpares = não divisível por dois (conjunto ℕ)
4- ………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
17- número primo = divisível apenas pela unidade e por sexo

Notamos imediatamente que alguns números na sequência possuem exatamente a propriedade à qual estão associados. Por exemplo:

1 possui exatamente a propriedade de ser um positivo natural
3 não é divisível por dois (permanecendo no conjunto ℕ)
17 tem a propriedade de ser divisível apenas por si mesmo e pela unidade

enquanto outros números estão associados a propriedades que não possuem. Por exemplo: 2 ≠ “é um quadrado perfeito”. Já os números que NÃO possuem a propriedade a que estão associados são definidos como Richardianos enquanto, obviamente, aqueles que a possuem são definidos como NÃO Richardianos.

A propriedade de ser ou não ser Richardiano é uma propriedade dos números Naturais portanto também pode fazer parte da lista de propriedades dos Naturais e nesta lista terá um número R = sendo um número Richardiano. R é um número Richardiano ou não? Este é o problema paradoxal de Jules Richard.

Se R fosse Richardiano não deveria estar associado à propriedade de ser Richardiano, enquanto se não fosse Richardiano não poderia estar associado à propriedade “ser um número Richardiano”. Naturalmente "ser ou não ser Richardiano" é uma propriedade NÃO Aritmética dos Números Naturais, portanto não poderia ser admitida na lista contável e numerada de propriedades matemáticas (de qualquer axiomatização da Aritmética); isso reduz a pseudoprova de Jules Richard a um Paradoxo.

Se R é Richardiano então não possui propriedades Richardianas

se não tiver as propriedades de Richardianos, não poderá entrar na lista de Richardianos

A autorreferencialidade parece evidente quando R = Richardiano é usado para demonstrar que R ≠ Richardiano enquanto a circularidade é destacada pelo minigráfico anterior.

Teorema de Turing

O Teorema de Alan Turing afirma a existência de algoritmos cuja computabilidade (verdade) não pode ser estabelecida porque geram um loop infinito (Problema de Parada).

Seja A um algoritmo operando em uma determinada entrada; o Teorema diz respeito à possibilidade de estabelecer se A(d) (calculabilidade de A no dado d) para em um tempo finito, ou seja, após um número finito de passos). Seja então um segundo algoritmo AR implementado em uma metalinguagem digital, tal que:

AR (A(d)) tem como saída V= verdadeiro ou F= falso

isto é, um algoritmo AR que estabelece através de uma saída (True) que A(d) terminará em um tempo finito, ou estabelece através da saída (False) que A(d) produzirá um loop infinito.

Em breve

se AR (A(d)) = verdadeiro então A(d) termina (para em um tempo finito)
se AR (A(d)) = falso então A(d) não termina (não para em tempo finito).

Dado que A e d são cadeias de símbolos de uma metalinguagem tendo como alfabeto 0, 1 (no caso de um alfabeto digital binomial) e, portanto, mutuamente intercambiáveis (não reconhecíveis como programa e entrada, mas apenas como sinais digitais), é possível para operar em l 'algoritmo AR obtendo AR ((A,(A))

AR (A(A)) verdadeiro se A(A) termina pela relação (1)
AR (A(A)) falso se A(A) não para em um tempo finito para a relação (2)

Agora repita a mesma operação realizada para a criação de (A,A) criando NW(AR, AR) que fornece a saída "verdadeira" se AR (A (A(d)) = não termina (conforme (2)) portanto: NW (AR, AR) é um programa que se define como "verdadeiro" se AR se define como "falso" que, por sua vez pela relação (2) define A(d) como um algoritmo que não termina (loop infinito ) Conclusão: Não pode haver um algoritmo que termine com True ou False (Stop) .

A técnica de demonstração é a da autorreferencialidade, poderosamente utilizada na avaliação de AR(AA) e NW(AR, AR) onde tanto o algoritmo AR se avalia em função do algoritmo A quanto do algoritmo NW.

Conclusão sobre o Teorema de Turing

(Onde, como sempre, nada é concluído, apenas destaca algumas curiosidades da pseudo lógica humana e do pseudo poder de uma SuperAI).

No final da década de 1930, Alonzo Church e Alan Turing publicaram o resultado do trabalho (conduzido separadamente e de forma independente, mas em última análise unificado com um resultado idêntico) destinado a resolver o agora antigo 10º problema de Hilbert e, em paralelo, o problema do Super IA. A conjectura deles é:

Se um problema for calculável humanamente, então haverá uma máquina de Turing capaz de resolvê-lo.

Alan Turing provou que não existe algoritmo, muito menos máquina, que possa resolver qualquer coisa que a mente humana possa resolver. Ainda mais analiticamente: se quiséssemos criar um algoritmo que estabeleça a priori se os programas de processamento de dados e autoaprendizagem do SuperIA poderiam ser um perigo para o gênero Homo Sapiens, obteríamos como resultado que este algoritmo hipotético (implementado em um A Máquina de Turing não é determinística) continuaria para sempre sem nunca dar uma resposta Verdadeira ou Falso.

O artigo Teorema de Turing: é por isso que nenhum algoritmo pode nos dizer se uma IA agirá contra a humanidade foi escrito em: Tech CuE | Engenharia de perto .