7 algoritmos que todo programador deve conhecer
Como estudante de programação, você provavelmente aprendeu muitos algoritmos diferentes ao longo de sua carreira. Tornar-se proficiente em diferentes algoritmos é absolutamente essencial para qualquer programador.
Com tantos algoritmos, pode ser um desafio acompanhar o que é essencial. Se você estiver se preparando para uma entrevista ou simplesmente aprimorando suas habilidades, esta lista o tornará relativamente fácil. Continue lendo enquanto listamos os algoritmos mais essenciais para programadores.
1. Algoritmo de Dijkstra
Edsger Dijkstra foi um dos cientistas da computação mais influentes de seu tempo e contribuiu para muitas áreas diferentes da ciência da computação, incluindo sistemas operacionais, construção de compiladores e muito mais. Uma das contribuições mais notáveis de Dijkstra é a engenhosidade de seu algoritmo de caminho mais curto para gráficos, também conhecido como Algoritmo de caminho mais curto de Dijkstra.
O algoritmo de Dijkstra encontra o caminho único mais curto em um gráfico de uma fonte para todos os vértices do gráfico. Em cada iteração do algoritmo, um vértice é adicionado com a distância mínima da fonte e um que não existe no caminho mais curto atual. Esta é a propriedade gananciosa usada pelo algoritmo de Djikstra.
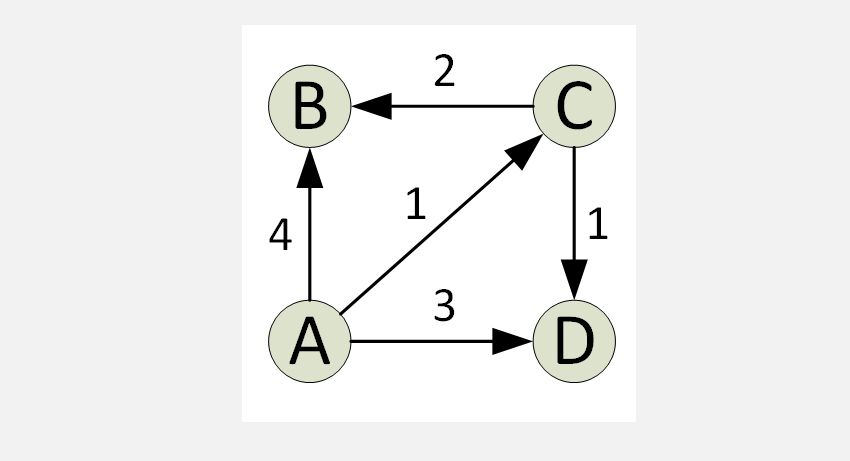
O algoritmo é normalmente implementado usando um conjunto. O algoritmo de Dijkstra é muito eficiente quando implementado com um Min Heap; você pode encontrar o caminho mais curto apenas no tempo O (V + ElogV) (V é o número de vértices e E é o número de arestas em um dado gráfico).
O algoritmo de Dijkstra tem suas limitações; ele só funciona em gráficos direcionados e não direcionados com arestas de peso positivo. Para pesos negativos, o algoritmo Bellman-Ford é normalmente preferível.
As perguntas da entrevista geralmente incluem o algoritmo de Djikstra, portanto, recomendamos a compreensão de seus detalhes e aplicações intrincados.
2. Mesclar Classificar
Temos alguns algoritmos de classificação nesta lista, e a classificação por mesclagem é um dos algoritmos mais importantes. É um algoritmo de classificação eficiente baseado na técnica de programação Divide and Conquer. Em um cenário de pior caso, a classificação por mesclagem pode classificar “n” números apenas no tempo O (nlogn). Em comparação com técnicas de classificação primitivas, como Bubble Sort (que leva O (n ^ 2) tempo), a classificação por mesclagem é extremamente eficiente.
Na classificação por mesclagem, a matriz a ser classificada é repetidamente dividida em submatrizes até que cada submatriz consista em um único número. O algoritmo recursivo então mescla repetidamente as submatrizes e classifica a matriz.
3. Quicksort
Quicksort é outro algoritmo de classificação baseado na técnica de programação Divide and Conquer. Nesse algoritmo, um elemento é escolhido primeiro como o pivô e toda a matriz é então particionada em torno desse pivô.
Como você provavelmente já deve ter adivinhado, um bom pivô é crucial para uma classificação eficiente. O pivô pode ser um elemento aleatório, o elemento de mídia, o primeiro elemento ou mesmo o último elemento.
As implementações do quicksort geralmente diferem na maneira como escolhem um pivô. No caso médio, o quicksort classificará uma grande matriz com um bom pivô em apenas tempo O (nlogn).
O pseudocódigo geral do quicksort particiona repetidamente o array no pivô e o posiciona na posição correta do subarray. Ele também posiciona os elementos menores que o pivô à sua esquerda e os elementos maiores que o pivô à sua direita.
4. Primeira pesquisa de profundidade
Depth First Search (DFS) é um dos primeiros algoritmos de gráfico ensinados aos alunos. DFS é um algoritmo eficiente usado para percorrer ou pesquisar um gráfico. Ele também pode ser modificado para ser usado na travessia da árvore.
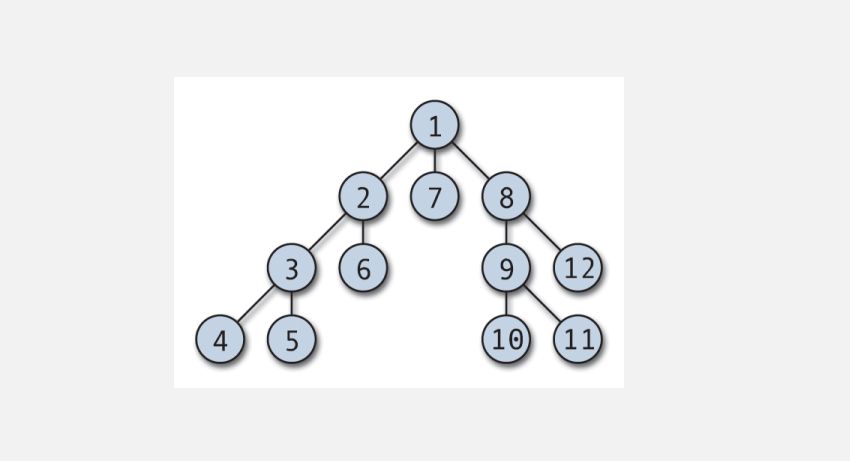
A travessia DFS pode começar a partir de qualquer nó arbitrário e mergulhar em cada vértice adjacente. O algoritmo retrocede quando não há vértices não visitados ou quando há um beco sem saída. O DFS é normalmente implementado com uma pilha e uma matriz booleana para manter o controle dos nós visitados. O DFS é simples de implementar e excepcionalmente eficiente; funciona (V + E), onde V é o número de vértices e E é o número de arestas.
As aplicações típicas do percurso DFS incluem classificação topológica, detecção de ciclos em um gráfico, localização de caminhos e localização de componentes fortemente conectados.
5. Pesquisa ampla primeiro
A pesquisa em amplitude (BFS) também é conhecida como uma travessia de ordem de nível para árvores. O BFS funciona em O (V + E) semelhante a um algoritmo DFS. No entanto, o BFS usa uma fila em vez da pilha. O DFS mergulha no gráfico, enquanto o BFS percorre o gráfico em sua amplitude.
O algoritmo BFS utiliza uma fila para rastrear os vértices. Os vértices adjacentes não visitados são visitados, marcados e enfileirados. Se o vértice não tiver nenhum vértice adjacente, um vértice será removido da fila e explorado.
O BFS é comumente usado em redes ponto a ponto, caminho mais curto de um gráfico não ponderado e para encontrar a árvore de abrangência mínima.
6. Pesquisa Binária
A pesquisa binária é um algoritmo simples para encontrar o elemento necessário em uma matriz classificada. Ele funciona dividindo repetidamente a matriz pela metade. Se o elemento necessário for menor do que o elemento intermediário, o lado esquerdo do elemento intermediário será processado posteriormente; caso contrário, o lado direito é dividido pela metade e pesquisado novamente. O processo é repetido até que o elemento necessário seja encontrado.
O pior caso de complexidade de tempo da pesquisa binária é O (logn), o que a torna muito eficiente na pesquisa de matrizes lineares.
7. Algoritmos de árvore de abrangência mínima
Uma árvore de abrangência mínima (MST) de um gráfico tem o custo mínimo entre todas as árvores de abrangência possíveis. O custo de uma árvore geradora depende do peso de suas arestas. É importante observar que pode haver mais de uma árvore de abrangência mínima. Existem dois algoritmos MST principais, nomeadamente o de Kruskal e o de Prim.
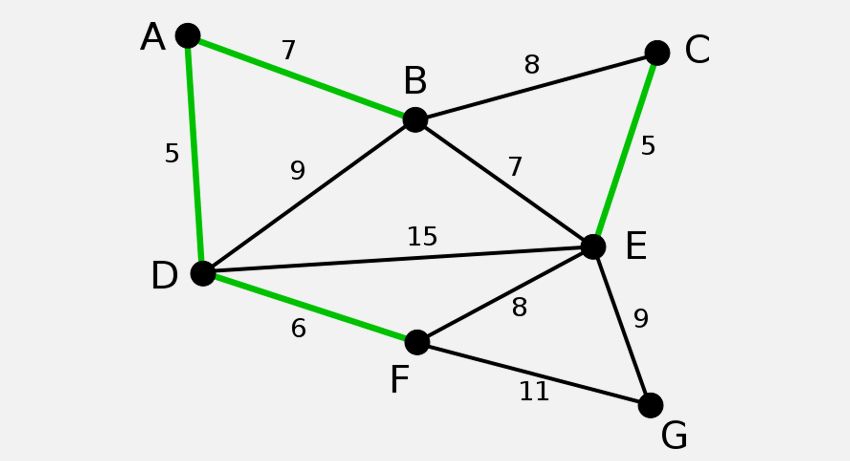
O algoritmo de Kruskal cria o MST adicionando a aresta com custo mínimo a um conjunto crescente. O algoritmo primeiro classifica as arestas por seu peso e, em seguida, adiciona arestas ao MST começando do mínimo.
É importante notar que o algoritmo não adiciona arestas que formam um ciclo. O algoritmo de Kruskal é preferido para gráficos esparsos.
O algoritmo de Prim também usa uma propriedade gulosa e é ideal para gráficos densos. A ideia central no MST de Prim é ter dois conjuntos distintos de vértices; um conjunto contém o MST crescente, enquanto o outro contém vértices não utilizados. Em cada iteração, a borda de peso mínimo que conectará os dois conjuntos é selecionada.
Algoritmos de árvore de abrangência mínima são essenciais para análise de cluster, taxonomia e redes de transmissão.
Um programador eficiente é proficiente em algoritmos
Os programadores aprendem e desenvolvem constantemente suas habilidades, e há alguns fundamentos básicos nos quais todos precisam ser proficientes. Um programador habilidoso conhece os diferentes algoritmos, as vantagens e desvantagens de cada um e qual algoritmo seria mais apropriado para um determinado cenário.

